
The Joke
Milk production at a dairy farm was at an all-time low, so the farmer decided to call on the local university for help. A team of the institutions' top scientists was assembled to work on the problem. The team of scientists visited the farm and took extensive data carefully examining every step of the production process. The leader of the team, a theoretical physicist, offered to write the report. A week later the physicist returned to the farm, saying to the farmer, "I have found a solution for your problem, but it only works for spherical cows in vacuum."
The Spherical Cow and Modeling
This joke appears in many variations. On "The Big Bang Theory," Sheldon Cooper delivers a version of it, but with chickens. There's also a great environmental science book by John Harte that focuses on order of magnitude type estimations titled Consider A Spherical Cow.
The joke is designed to poke fun at theorists for making unrealistic assumptions in order to simplify a problem to make it easier to solve (or solvable at all). This is so pertinent in the physics classroom because as physics teachers we are CONSTANTLY making assumptions that are obviously untrue (i.e. frictionless surface, massless pulley, uniform density, no air drag, neglect gravitational effects... the list goes on).
In my classroom, I bring up spherical cows when I introduce experimental error. The concept serves as a nice starting point in discussing how students should often approach writing error analyses. I encourage students to focus on determining exactly what their model incorporates. Then they can begin to craft an analysis that is founded upon discrepancies between the physical model they are using and the real-world system they are studying.
We have a tendency to rush in and apply the model without taking time to encourage students to recognize that the model is just a model--not the real thing. By encouraging students to focus on the discrepancies between the physical model and their experimental system, they learn how to craft more sophisticated analyses. I like to call this process "model breaking." They also learn implicitly that physics is a toolkit of models that represent real life. Tools that have varying degrees of relevancy and accuracy depending on how they are applied.
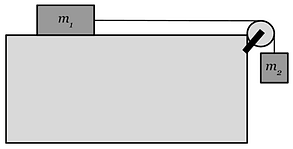
An Example: Atwood's Machine
Consider the lab setup shown below:

Now consider a physical model that would be used to describe this system if taking a Newton's Laws/Forces approach:
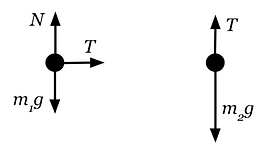
Let's say students have already learned Newton's Laws and they have been given the masses of the cart and the hanging weight. A simple experiment might be asking students to predict the acceleration of this system given m1 and m2 and then experimentally verify it. For a more sophisticated experiment, students could derive an equation relating the system's acceleration to m1 and m2 and then do controlled experiments with one of these masses as the independent variable with the goal of comparing their theoretically determined curve with their experimental one. In either case, students are likely to observe that acceleration data comes out less than what their model predicts.
Model-Breaking Brainstorm:
Taking time for a post-lab brainstorm discussion after the experiment gives students an opportunity to collaboratively recognize where their model deviates from the experimental apparatus. By prompting students with questions like "Okay, what is the physical model we used to study this system?", "Which objects and forces did we include in our physical model?", or "What factors did we fail to account for in our physical model?" Students can work together to come up with a list of possible discrepancies.
For this system, students could list some of the following:
-
They neglected air drag.
-
They ignored the rotation of the pulley (Doesn't the pulley require an unbalanced force in order to start spinning???)
-
The cart has wheels (it's not sliding) does this make a difference?
-
There's friction against axles in the cart's wheels and on the pulley.
-
The string has mass contributing to the inertia of the system.
Now students can go back to their data and consider how ignoring these properties may be causing the physical model yield acceleration values that are greater than experimentally determined values.
Model Breaking and Experimental Outcomes
The meat of this "model breaking" error analysis is not in just listing these sources of error but in guiding students to determine:
-
Which sources of error are truly significant?
-
How do those sources affect experimental outcomes?
This process becomes more challenging with more complex systems. Depending on the lab, students may be simply comparing an experimental and predicted value or they may be discussing how a predicted/theoretical graph compares to their experimental graph. Students should eventually be able to use these discrepancies to make quantitative comparisons between their experimental and theoretical graphs or to make conjectures about whether experimentally determined constants are higher/lower than their actual values.
.png)
